大阪府東淀川区にある瑞光中学校専門塾の瑞光ゼミナールです。

この記事を読めば…

• 中1の四則混合計算 → 中2の文字式の乗法 → 中3の分配法則・因数分解 とつながる考え方がわかります

• 逆向きの 因数分解 が“片付け”感覚で身につく

---

1. 分配法則って何？

数学の教科書にはこう書いてあります。

a(b+c)=ab+ac

でも、文字だけだとピンとこないですよね。そこで “セットをばらす” というイメージを持ちましょう。

1‑1 お弁当の例

状況：お弁当が 2 個。中身は おにぎり1個 + 卵焼き1個。

式：2(おにぎり+卵焼き)

開けて並べると → 2おにぎり + 2卵焼き

ポイント：掛け算の 2 が “弁当を 2 つ開けていく” 動作になっている。

1‑2 洋服たたみの例

状況：3 人分の洗濯物。1 人あたり シャツ + ズボン + 靴下。

式：3(シャツ + ズボン + 靴下)

ばらして畳む と → 3シャツ+ 3ズボン + 3靴下

 

1‑3 面積モデルで公式を確認

長方形を b と c に分け、高さ a をかけると…。

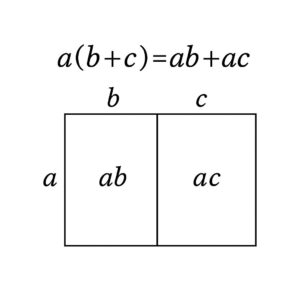
面積の合計が ab + ac になることで、公式が視覚的に納得できます。

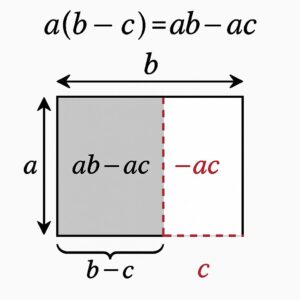
分配法則の 引き算版 では、まず「全体が ab、そこから ac を取り除く」感覚をつかむと一気にラクになります。

 

---

 

２. 因数分解は“まとめ直し”

散らばったものを箱に戻すイメージです。

3‑1 お弁当リバース

おにぎり 2 個 + 卵焼き 2 個 → 同じセットが 2 つ
2おにぎり+ 2卵焼き= 2(おにぎり + 卵焼き)

3‑2 洋服たたみリバース

3シャツ + 3ズボン + 3靴下 = 3(シャツ + ズボン + 靴下)

 

 

---

3. まとめ & 次のステップ

分配法則は セットをばらす 動作

因数分解は ばらばらを箱にまとめる 処理

イメージ化すると計算手順が体に染みつく